Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.
Llamamos cuerpos de revolución a los cuerpos que se obtienen al girar una figura plana alrededor de un eje.
Prueba lo siguiente:
|
Formas
en cartulina |
Girar |
Cuerpos que se forman |
 |
|
Cilindro | |
 |
 |
Cono | |
 |
 |
Tronco de cono |
|
 |
 |
Diábolo |
Eje
El eje del cono es el cateto fijo alrededor del cual gira el triángulo.
Base
La base del cono es el círculo que forma el otro cateto.
Altura
La altura del cono es la distancia del vértice a la base.
Generatriz
La generatriz del cono es la hipotenusa del triángulo rectángulo.
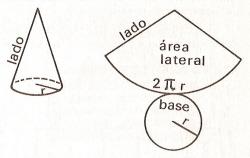
El desarrollo plano de un cono recto es un sector circular y un círculo.
El sector circular está delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base.
Área lateral y total del cono.
El área lateral
de un cono es el producto
de la longitud de la circunferencia de la base por el lado o generatriz,
dividido por 2.
Área lateral del cono = ( 2 x p
x r ) x lado / 2.
El área total
es la suma del área lateral más el área del círculo de la base.
Área total del cono = área lateral + área de la base.
Donde 
es el área de la base del conoEl volumen del cono es la tercera parte del volumen del cilindro,
Por lo tanto la fórmula es la siguiente:
No hay comentarios:
Publicar un comentario