Cálculo de áreas de las figuras planas.
El punto de partida para la determinación del método aritmético de
cálculo de la medida de la superficie comprendida en las figuras
geométricas planas, es el estudio del cuadrado.
Subdividiendo un cuadrado en varios cuadrados cuyo lado sea una parte
del cuadrado original, resulta fácil apreciar que la cantidad de
cuadrados menores — que pueden considerarse como unidad de medida — es
igual a la multiplicación del número de cuadrados contenidos en dos de
los lados del cuadrado originario: 5 × 5 = 25.
Conviniendo en denominar base al lado horizontal del cuadrado original, y
altura el vertical; el procedimiento de cálculo de la superficie del
cuadro puede expresarse en la fórmula:
SUPERFICIE DEL CUADRADO = BASE × ALTURA
En el caso del rectángulo, el mismo procedimiento permite establecer que
el procedimiento de cálculo de su superficie es igual al del cuadrado: 5
× 8 = 40.
SUPERFICIE DEL RECTÁNGULO = BASE × ALTURA
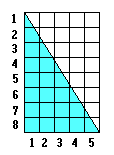 La
fórmula de cálculo del área del triángulo, es una derivación de las
anteriores, atendiendo a que la diagonal de rectángulos lo divide en dos
triángulos; por lo cual la superficie de todo triángulo es igual a la
mitad de la del polígono que resultaría de duplicarlo tomando uno de sus
lados como eje de simetría: 5 × 8 = 40 ÷ 2 = 20.
La
fórmula de cálculo del área del triángulo, es una derivación de las
anteriores, atendiendo a que la diagonal de rectángulos lo divide en dos
triángulos; por lo cual la superficie de todo triángulo es igual a la
mitad de la del polígono que resultaría de duplicarlo tomando uno de sus
lados como eje de simetría: 5 × 8 = 40 ÷ 2 = 20.
Si se observa un trapecio, se percibe que cada una de sus diagonales lo convierte en la suma de dos triángulos.
Por lo tanto, la superficie de un trapecio es la suma de las
superficies de uno de los dos pares de triángulos que se forman al
trazar una diagonal.
En el trapecio, se denomina base mayor al mayor de sus lados paralelos, y
base menor al otro lado paralelo. De tal manera, la base mayor resulta
ser la base de uno de los triángulos, y la base menor resulta ser la
base del otro; en tanto que la altura del trapecio es la altura de ambos
triángulos. Puede obtenerse la suma de ambas superficies en una única
operación, sumando ambas bases, dividiendo el resultado entre 2, y
multiplicando por la altura: 9 + 6 = 15 ÷ 2 = 7,5 × 5 = 37,5.
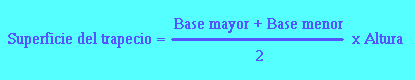

No hay comentarios:
Publicar un comentario